
GCSE Revision Guides for Science Subjects – Order Online
Chemistry, Biology, Physics, and Maths by Example
Are you anxious about your upcoming GCSE science and maths exams?
The Learn by Example series are complete GCSE science revision guides which show how to tackle exam questions in a multitude of subjects. With each problem broken down and fully worked, you can practice and follow the guidance and have the techniques in your armoury in time for your exams.
All our books have been written by existing or recently retired teachers and tutors. This is unique to Prichard Guides, no other company uses exclusively teachers and tutors to produce their materials.

The By Example series features:
- Over 200 questions in each guide with fully worked answers are laid out in simple step by step fashion to give you real understanding.
- Hints and tips in each AQA GCSE revision guide on how you approach questions so you will be ready for real exams.
- Self-testing sections at the end of each unit, so you can test your knowledge.
- Clear diagrams, graphs and equations are included, for effective learning.
- Examples of test questions are included, to ensure you are totally prepared.
- Covers everything on the Science AQA syllabus from grades 9-1, and the maths syllabus grades 1-5, so you won't need anything else.

Prichard Guides You With Answers...
Hello, my name is Tim Prichard and I am a former Head of a Science Faculty in a secondary school in Somerset, England. I have taught science in a broad range of schools across the UK and abroad for nearly 30 years, to all ages and abilities. I am currently using my background in science, working at the University of Bath at the Chemistry Department.
Over the years, the science GCSE curriculum has often changed in both content and focus. We have witnessed the introduction of coursework, modular exams and practical assessments, and now we have gone full circle with the return of linear end-of-course exams. I have taught through all of these changes.
The literature to support students' learning has constantly evolved to keep pace with the changing nature of education. In my experience, I believe that the best way to assist students in consolidating their learning and embedding their knowledge is through practice. So, I wrote my own GCSE science revision guides to do just this – Physics by Example, Chemistry by Example, and Biology by Example, all based on the UK's AQA syllabus. A foundation Maths text book has also being written by the head of a Maths faculty.
All of the questions in these online and print revision guides for GCSE have been tried and tested over three decades in the classroom, and they've proven very successful in helping my students to learn and understand Physics, Chemistry, Biology and Maths. I am absolutely confident you will achieve success by using the same material now published in this guide.
I very much hope you, teachers, students and parents alike, will find the approach taken by this AQA GCSE science guide as helpful as my students have over the years.
Tim Prichard
What We Offer

Physics GCSE
This is a complete revision guide for all the current AQA GCSE Physics courses including the Trilogy, Synergy and Physics GCSE.

Chemistry GCSE
This provides a successful way of consolidating and reaffirming scientific facts and concepts for students who are studying GCSE Chemistry.

Biology GCSE
This guide is a proven aide to remembering and reaffirming scientific facts and concepts for students who are studying GCSE Biology.

Maths GCSE
This Maths GCSE revision guide offers more than 200 illustrative questions accompanied by comprehensive step-by-step solutions.
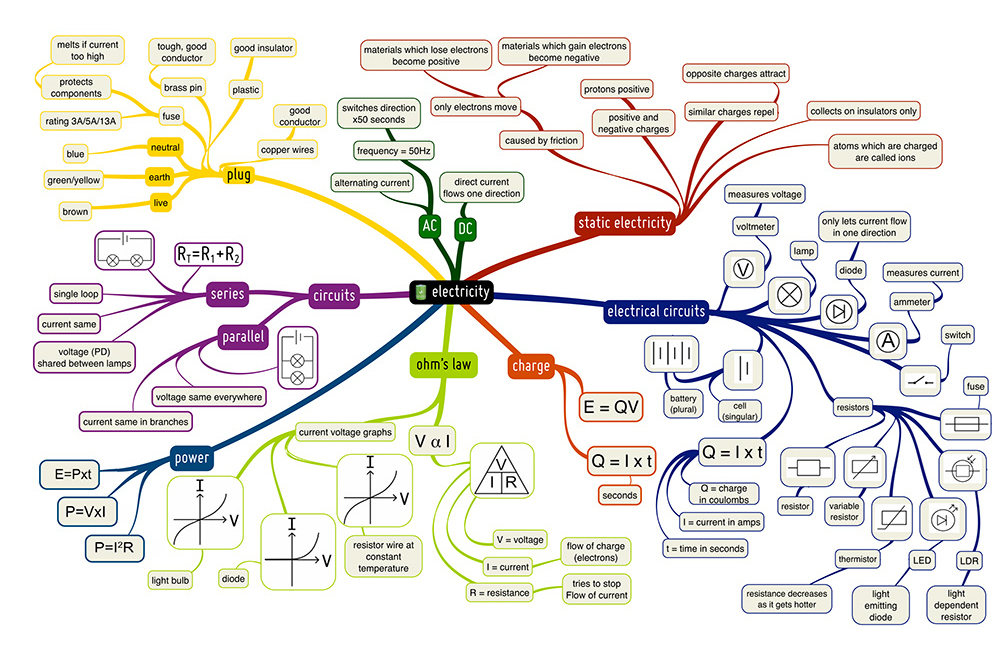
Mind Maps
We have composed a range of mind-maps for the different topics in each subject, enabling students to recall ideas and information more readily. (Currently only available for the sciences.)
What Careers Require These Qualifications?
Science subjects and qualifications can open up a wealth of opportunities for the future. Take a look at examples of career paths each of these science GCSE subjects could start students on a path towards.
Physics
- All types of engineering from acoustics to agricultural
- Air traffic control
- Chartered surveyor
- Computer programming
- Environmental scientist
- Geologist
- Doctor
- Architect
- Pharmacist
- Radiographer
- Water management
- Health services
Chemistry
- Laboratory Technician
- Firework Designer
- Water management
- Forensics
- Brewing and Distilleries
- Veterinary Nurse
- Doctor
- Car manufacture
- Paint and dye manufacture
- Nurse or Paramedic
- Environmental protection
- Food standards
- Fragrance and cosmetics design
- Drug and medicine design
Biology
- Medical doctor
- Pharmacist
- Biomedical Scientist
- Veterinarian
- Forensic Scientist
- Botanist
- Ecologist
- Zoologist
- Biotechnologist
- Environmental Scientist
Maths
- Actuary
- Statistician
- Data Analyst/Data Scientist
- Quantitative Analyst
- Mathematics Teacher/Educator
- Operations Research Analyst
- Financial Analyst
- Software Developer/Programmer
- Economist
- Engineer (Various Fields)
- Market Research Analyst
- Logistician
- Physics/Mathematics Researcher
- Urban Planner

Why buy my books/eBooks?
During revision for her own GCSE exams, my daughter pointed out to me that many of the existing guides lacked working examples of problem solving. This made it difficult to know where to begin when tackling an exam question, and which formulae to use, for example. While most guides had a couple of examples, this is not sufficient, and does not cover the topic adequately.
Having taught Physics and Chemistry for many years I am fully aware that when a student is preparing for an examination it is critical that they practice answering questions and fully understand the methodology needed to answer the question.
These GCSE revision guides have every step written down, so the student can transfer these methods to other questions. Each one has over 200 fully worked examples for all topics covering grades 9-1 on the UK's current AQA syllabus.
All of our eBooks, can be downloaded from online onto the most popular formats, such as Kindle and iPhone, and you can always have them with you, handy for impromptu revision.
Shop Revision Guides Shop Mind Maps
Testimonials
“Very helpful, and the examples were explained very well.”
Megan Sellars
“I really liked physics by example because the information is easy to understand and shows examples of how to work out questions.”
George Baker
“Very helpful. I liked how there were self testing questions, with space to work them out.”
Alice Reilly
“Physics by example made revision simple and easy. It is well laid out, and I liked the practice questions.”
Connor Hood


